Introducing Complexity and Generics using a Linked List
Limitation of arrays
Although arrays are useful data structures, they have limitations:
- the size of the array is fixed at compile time.
- When overflow happens, a copy of the old array is needed.
- the data elements are physically arranged in memory next to each other. This has both advantages and limitations.
How to compare different data structures?
We already studied array lists and arrays. How do we compare the performance of these data-structures, especially as we perform different operations such as inserting, deleting at different positions of the datastructure. To perform such comparisons without the need for actual implementations, the Big-O notation is used. Let’s see a few examples to illustrate the concept:
An informal introduction to Big-O
Thus O expresses an upper-bound on the total number of operations performed by some function or algorithm as a function of the number of inputs N.
- O(1) – a constant number of operations, that is independent of the input size.
- O(N) – the number of operations is a polynomial whose highest degree is N (linear).
- O(\(N^2\)) – the number of operations is a polynomial whose highest degree is \(N^2\) (quadratic), and so on.
if-statement, where the body is independent of the input size: O(1)
if (a < b) {
tmp = a;
a = b;
b = tmp;
}
for-loop, while-loop, with linear steps: O(N)
for (i = 0; i < N; i += 2)
for-loop, while-loop, with dividing/multiplying steps: O(logN)
for (i = 1; i < N; i*=2)
nested for-loop, linear steps: O(\(N^2\))
for (i = 0; i < N; i+=2)
for (j = 0; j < N; j++)
for-loop with function call… in this example: O(\(N\)logN)
for (i = 0; i < N; i+=2) // O(N)
divide(); // O(logN)
nested for-loop with function call… in this example: O(\(N^3\)logN)
for (i = 0; i < N; i++) // O(N)
for (j = 1; j < N; j*=2) // O(logN)
bubbleSort(list); // O(N*N)
Array complexity
-
Adding a new element: O(N), copying all elements to a larger array
-
Deleting an element: O(N) if in middle/front, O(1) at the end
-
Retrieving an element at a particular index: O(1)
Array list complexity
- Adding new value: O(1) amortised (on average) if doubling
size… N insertions, and doubling array k times, to fit N elements
(so N \(\approx {2^k}\))
- Total cost: \(N + 2^1 + 2^2 + 2^3 + ... + 2^{k-1} + 2^k \\\rightarrow N + 2\times2^k (since \sum(2^1 + 2^2 + 2^3 + ... + 2^{k-1}) \approx 2^k) \\\rightarrow N + 2N \\\rightarrow O(N)\)
- The total cost is O(N), amortized to O(1) over N operations
Linked-list complexity
-
Add/delete at front: O(1)
-
Add/delete at end, without knowing tail: ?
-
Add at end, with knowing tail: ?
-
Delete at end, with knowing tail, without access to prev node: ?
-
Delete at end, with knowing tail, with access to prev node: ?
-
Add/delete in middle: ?
-
Retrieving an element at a particular index: ?
Linked List building block – a Node
- A
Nodeis an object which consists of avalueand a reference to thenextNode. - Here is a potential implementation:
public class Node {
private int val;
private Node next;
// constructor
public Node(int v) {
val = v;
next = null;
}
// getters and setters
public void setNext(Node n) {
next = n;
}
public Node getNext() {
return next;
}
public int getValue() {
return val;
}
public static void main(String args[]) {
Node n1 = new Node(0);
Node n2 = new Node(200);
Node n3 = new Node(-50);
n1.setNext(n2);
n2.setNext(n3);
n3.setNext(null);
Node n = new Node();
n = n1;
while (n != null) {
System.out.println("The value of the next node is: " + n.getValue());
n = n.getNext();
}
}
}
What are the limitations of the above Node?
- The
Nodestores integer values only. What we need to store other types? - There are problems with the main method as well. We will defer this discussion to later.
However, isn’t this problem easy to fix, since Java supports the concept of Objects. Here is a revision of the previous implementation.
public class Node {
private Object val;
private Node next;
// constructor
public Node() {
}
public Node(Object v) {
val = v;
next = null;
}
// getters and setters
public void setNext(Node n) {
next = n;
}
public Node getNext() {
return next;
}
public Object getValue() {
return val;
}
public static void main(String args[]) {
Node n1 = new Node(0);
Node n2 = new Node(200);
Node n3 = new Node(-50);
n1.setNext(n2);
n2.setNext(n3);
n3.setNext(null);
Node n = new Node();
n = n1;
Double sum = 0.0;
while (n != null) {
System.out.println("The value of the next node is: " + n.getValue());
sum = sum + ((Double) n.getValue());
n = n.getNext();
}
System.out.println("The sum of the values: " + sum);
}
}
What problem do you find with this approach?
Generics
- The key idea is to support parametric types
- Thus, classes, interfaces operate on data-types, which can be changed like a parameter.
- Classes, interfaces and methods operating on parametric types are called generic classes, interfaces or methods.
- Allows us to define a data-structure or algorithm once, which is agnostic to the data-types it will operate on.
- Ensure type-safe operation
Terminology used for Java Types
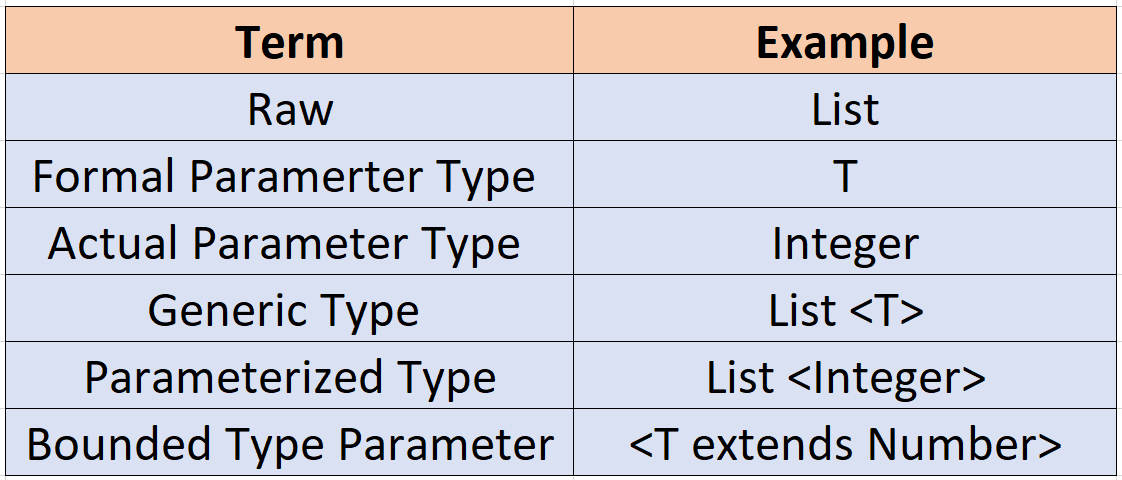
Type safety with Java Generics
- For a review of Java data types examine the following link
- One of the main benefits of generics is to ensure type safety
- Type safety ensures that expressions and assignments are done using consistent types
- This ensures that what the programmer intends at compile time happens at run time.
- Here is how the previous program is revised using Java generics to ensure type safety
- NOTE: In the following
Tcan’t be a primitive type but has to be a reference type i.e. you can use any object except built in data types such asint,floatetc.
public class Node<T> {
private T val;
private Node<T> next;
// constructor
public Node() {
}
public Node(T v) {
val = v;
next = null;
}
// getters and setters
public void setNext(Node<T> n) {
next = n;
}
public Node<T> getNext() {
return next;
}
public T getValue() {
return val;
}
public static void main(String args[]) {
Node<Integer> n1 = new Node<Integer>(0);
Node<Integer> n2 = new Node<Integer>(200);
Node<Integer> n3 = new Node<Integer>(-50);
n1.setNext(n2);
n2.setNext(n3);
n3.setNext(null);
Node<Integer> n = new Node<Integer>();
n = n1;
Double sum = 0.0;
while (n != null) {
System.out.println("The value of the next node is: " + n.getValue());
sum += n.getValue();
n = n.getNext();
}
System.out.println("The sum of the values: " + sum);
}
}
How about adding node values of different types
public class Node<T> {
private T val;
private Node<T> next;
// constructor
public Node() {
}
public Node(T v) {
val = v;
next = null;
}
// getters and setters
public void setNext(Node<T> n) {
next = n;
}
public Node<T> getNext() {
return next;
}
public T getValue() {
return val;
}
public static void main(String args[]) {
Node<String> n1 = new Node<String>("se");
Node<String> n2 = new Node<String>("2");
Node<String> n3 = new Node<String>("8");
Node<String> n4 = new Node<String>("1 ");
n1.setNext(n2);
n2.setNext(n3);
n3.setNext(n4);
n4.setNext(null);
Node<String> n = new Node<String>();
n = n1;
String sum = "";
while (n != null) {
System.out.println("The value of the next node is: " + n.getValue());
sum = sum + n.getValue();
n = n.getNext();
}
System.out.println("The sum of the values: " + sum);
sum = sum + new Node<Object>(n1).getValue();
System.out.println("The next sum of the values: " + sum);
}
}
Bounded Types
public class Node<T extends Number> {
private T val;
private Node<T> next;
// constructor
public Node() {
}
public Node(T v) {
val = v;
next = null;
}
// getters and setters
public void setNext(Node<T> n) {
next = n;
}
public Node<T> getNext() {
return next;
}
public T getValue() {
return val;
}
public static void main(String args[]) {
Node<Integer> n1 = new Node<Integer>(0);
Node<Integer> n2 = new Node<Integer>(200);
Node<Integer> n3 = new Node<Integer>(-50);
n1.setNext(n2);
n2.setNext(n3);
n3.setNext(null);
Node<Integer> n = new Node<Integer>();
n = n1;
Double sum = 0.0;
while (n != null) {
System.out.println("The value of the next node is: " + n.getValue());
sum = sum + n.getValue();
n = n.getNext();
}
System.out.println("The sum of the values: " + sum);
sum += new Node<Double>(10.0).getValue();
System.out.println("The sum of the values: " + sum);
}
}
Linked List by linking nodes nodes (see above)
This approach is not good OO design. Here are some points why?
- A
Nodeis part of aLinkedListbut is not the list itself - The API of the Node class deals with method for a Node rather than for a list
- A
LinkedListmay be of many types, i.e. a singly linked list or a doubly linked list. Here we can use the familiar interfaces to ensure that both types have the same interface.
public interface List<T> {
public void append(T item);
public void prepend(T item);
public T fetch(int pos) throws InvalidPositionException;
public void insert(int pos, T data) throws InvalidPositionException;
public void remove(int pos) throws InvalidPositionException;
public int size();
public void print();
}
A first cut of the LinkedList class
 Get your hands dirty!
Get your hands dirty!
In the following you are given the first version of the LinkedList
that implements the List interface.
public class LinkedList<T> implements List<T> {
private Node<T> head;
public LinkedList() {
head = null;
}
// Key methods of the List interface
public void prepend(T data) {
// Note -- works even if list is empty
Node<T> n = new Node<T>(data);
n.setNext(head);
head = n;
}
public void append(T data) {
}
public T fetch(int pos) throws InvalidPositionException {
T val = head.getValue();
return val;
}
public void insert(int pos, T data) throws InvalidPositionException {
}
public void remove(int pos) throws InvalidPositionException {
}
public int size() {
int i = 0;
return i;
}
}
We will now do the following exercise in ACP:
- In ACP you are already given the test case for testing the
prependmethod for prepending integers. This fails. Why? - Implement the appropriate fix so that the test on the
prependmethod above passes - Add a test case for testing
prependworks for strings - A test case added for testing the
fetchmethod, which fails - Correct implementation of
fetchand other test cases for prepend - New test case for testing
prependandfetch, which passes - Test case for
appendthat fails - Prepend followed by append passes but test append fails. Why?
- Fix the
appendmethod - Refactoring to add a test case for a method called
locateNodeand the empty method in the class - Correct implementation of
locateNodewith appropriate test cases, which pass - Refactor all methods using the
locateNodemethod.
